Getting A Royal Flush
- Odds Of Getting A Royal Flush On The Flop
- Probability Of Getting A Royal Flush Equation
- What Are The Odds Of Getting A Royal Flush
/royal-flush-172214648-bafb6213188744e981412665b63b6be2.jpg)
The crème de la crème of almost every poker game is getting a Royal Flush. It’s not only a rare occurrence that can make jaws drop, but hitting a Royal Flush is usually something that will boost a bankroll by a ton. This is certainly the case in Video Pokers, which are simple games with potentially massive rewards.
But how much will you actually make if you happen to hit a Royal Flush at a casino playing Video Poker and what is the likelihood of doing so? These are just two of the questions that we will be answering in the following article, along with explaining the optimal strategy of drawing to a Royal Flush.
Before we get to this, though, let us start with the basics to make sure that you know what a Royal Flush actually is. Many gamblers wrongly confuse the hand with a straight flush. Let’s not make that mistake.
Regardless of how many players are participating in a game of Hold'em, there are 36 hands that can make a straight flush (remember, we need to exclude the four hand that make a royal flush). Now, there are 2,598,960 different hand combinations in Hold'em. The royal flush contributes 1.9807% toward the overall 99.64% return. The following table summarizes the contribution of each winning hand toward the overall 99.54% return (for 9/6 Jacks or Better). When you don’t hit the royal or straight flush, the best return you can expect, even playing perfectly, is about 97%. Got a video poker question? Royal flush definition is - a straight flush having an ace as the highest card. The royal flush is a case of the straight flush. It can be formed 4 ways (one for each suit).
The Difference Between a Straight Flush and a Royal Flush
As you may or may not already know, a straight in any 5-card poker game is made up of five cards that are sequentially connected to each other, while a flush is five cards that are all of the same suit (♥, ♠, ♦ or ♣). Logically, a straight flush is therefore five cards of the same suit that are sequentially connected to each other.
The same can actually be said about a Royal Flush, which is also a colored straight. However, this hand is only created if the colored straight is made up of the five highest cards in the deck. In other words, the 10, Jack, Queen, King and Ace. Thus, it is much more difficult to hit a Royal Flush in Video Poker than it is hitting just a straight flush.
These are some of the straight flushes in Video Poker:
- 2♥, 3♥, 4♥, 5♥, 6♥
- 9♠, 10♠, J♠, Q♠, K♠
- 5♦, 6♦, 7♦, 8♦, 9♦
- 7♣, 8♣, 9♣, 10♣, J♣
These are the only four Royal Flushes in Video Poker:
- 10♥, J♥, Q♥, K♥, A♥
- 10♠, J♠, Q♠, K♠, A♠
- 10♦, J♦, Q♦, K♦, A♦
- 10♣, J♣, Q♣, K♣, A♣
How Much Does a Royal Flush Payout in Video Pokers Online?
This depends on two things; the version of the game that you’re playing and the coin level that you’re playing with. Many of the best Video Poker casinos in the UK have several different variants that can be enjoyed, such as Jacks or Better, Deuces Wild, Joker Poker, Jackpot Poker, All Aces and All American.
All of these games also have five different coin levels, which is a betting option. No matter the Video Poker you’re playing, you’re betting coins and the coin level decides how many you’re betting (1, 2, 3, 4 or 5). To get the right stake, you can also adjust a coin value that sets the amount of real cash that each coin should be worth.
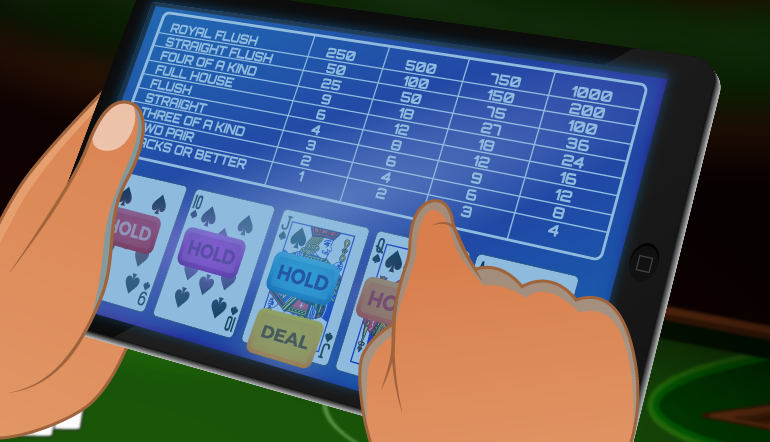
What’s important to know and what is illustrated in the below table, is that you must play with the highest coin level to be able to get the highest payout from a Royal Flush in Video Poker.
Please note that the above payouts are all listed as a multiplier to the stake that you’re playing with. So if you’re playing with a stake of £1 and get a 250x win from a Royal Flush, you would win £250.
As you can see, the payouts from a Royal Flush are very similar between the different Video Poker versions. The only one that stands out is Jackpot Poker which has the potential to pay a lot more. This game comes with a progressive jackpot that can pay tens of thousands of pounds if it’s been built up nicely. It also never pays any less than £5,000 as this is the jackpot’s starting value.
In Jackpot Poker the stake is only adjusted by the coin level and when this is set to the maximum one, you’re betting £5. This means that winning the jackpot will pay 1,000 times your stake at the very least and could potentially pay up to 10,000x.
These Are the Odds of Getting a Royal Flush in Video Poker
Like most gamblers, you’re probably wise enough to know that getting a Royal Flush while playing video poker is really difficult. Though, you may also think that it wouldn’t be too hard should you be spending a couple of hours on a session trying to achieve it. If you do believe this, you’re actually terribly wrong.
Let us assume that a hand of video poker takes 5 seconds to play. You would then be able to go through 12 hands every minute and 720 hands every hour. If you keep this up you would be expected to get your Royal Flush after playing straight for two days and 7 hours as the chance of hitting one is approximately 1 in 40,000 hands. This is probably way more than you thought, right?
While it may not be much of a comfort, we can tell you that you will come close to hitting one much more often. To illustrate this, let’s have a look at the chance of being dealt 1, 2, 3, 4 or 5 cards to a Royal Flush on the initial deal.
As you can see, playing for just an hour would yield you as many as 7 game rounds where you get teased by getting dealt three cards to a Royal Flush. And if you make your session a really long one and play for about four hours, you will even be dealt a hand where only a single card is missing from the big hand.
This might make you wonder what the chances are to hit the cards that you need after the initial deal. Well, let us answer this by taking a look at it!
| v2.1% | ||
The most interesting part is the 1 in 47 chance that you have whenever you’re initially dealt four cards to a Royal Flush. While this only happens once every four hours or so (on average), when it does you can actually feel the big hit coming. However, 1 in 47 is still only 1 in 47 so 46 out of 47 times you’re going to miss. No matter how we twist and turn the probabilities, the fact won’t change that a Royal Flush only happens once on every 40,000th hand.
Do note that all of the above probabilities are based on the game Jacks or Better. If you’re playing with wild cards such as in Joker Poker (this has an extra wild joker) and Deuces Wilds (in this all 2’s are wilds) your chances will obviously be increased.
When Is the Right Time to Draw to a Royal Flush? Here’s the Perfect Strategy!
Playing Video Poker, you will encounter a ton of hands where you get two or more cards to a Royal Flush. For instance, checking the tables that we have listed above, you can see that two cards to a Royal is dealt as often 1 in 13 hands. While you may be tempted to go for the big prize, only a few of these hands should actually be used to go for the Royal if you want to play optimally. To maximize your long-term chances of winning in the game, it is usually much better to break the Royal draw and go for another hand.
To help you out making the right decisions, we have listed all of the possible Royal draw scenarios and mentioned when you should and should not go for the draw. This Royal Flush strategy applies to Jacks and Better only and not to Deuces Wild or Joker Poker.
Please also note that whenever we use the term ‘high pair’ or ‘high cards’, this means a pair of jacks or better or cards that are either jacks or better. Similarly, the term ‘low pair’ or ‘low card’ means a pair of 10’s or worse or cards that are either 10 or lower.
These Are the Hands That You Should Draw to a Royal Flush
- Flush with one card from a Royal (2♥, 10♥, J♥, Q♥, K♥)
- Straight with one card from a Royal (10♥, J♥, Q♠, K♥, A♥)
- High Pair with one card from a Royal (10♥, J♥, Q♥, Q♠, K♥)
- Low Pair with three cards from a Royal (4♠, 10♠, 10♥, Q♥, K♥)
- One card from a flush with two cards from a Royal (2♠, 5♥, 10♥, Q♥, K♥)
- One card from a straight with two cards from a Royal (2♠, 10♠, J♥, Q♥, K♥)
- One card from an inside straight with two high cards to a Royal (2♥, 10♣, J♣, Q♥, A♥)
- Three high cards and two high cards to a Royal (2♠, 4♠, J♣, Q♥, K♥)
- Two cards from a straight flush and two high cards to a Royal (5♠, 6♠, 8♠, K♥, A♥)
These Are the Hands You Should NOT Draw to a Royal Flush
- Straight flush that is already made (9♥, 10♥, J♥, Q♥, K♥)
(keep the straight flush) - Three of a kind with three cards to a Royal (J♥, Q♥, Q♠, Q♣, K♥)
(keep the three of a kind) - Flush with two cards from a Royal (2♥, 6♥, J♥, Q♥, K♥)
(keep the flush) - Straight with two cards from a Royal (10♥, J♥, Q♥, K♠, A♠)
(keep the straight) - Two Pair with two cards from a Royal (10♥, 10♠, J♥, J♠, Q♥)
(keep the two pair) - High Pair with two cards from a Royal (3♠, 10♥, J♥, Q♥, Q♠)
(keep the pair) - One card from a flush with three cards from a royal (2♠, 7♥, 8♥, Q♥, K♥)
(go for the flush) - Low pair with three cards from a royal (3♥, 6♠, 6♣, J♥, Q♥)
(keep the pair) - One card from an outside straight with three cards from a royal (2♣, 9♣, 10♠, J♥, Q♥)
(go for the straight) - Two cards from a straight flush with three cards from a royal (4♣, 5♣, 6♣, J♥, Q♥)
(go for the straight flush) - One card from a high inside straight with three cards from a Royal (7♣, 10♠, J♣, K♥, A♥)
(go for the straight) - Two cards from a straight flush and two cards to a Royal with a 10 included (2♠, 4♠, 7♥, 10♥, J♥)
(go for the straight flush) - Two high cards and two cards to a Royal with a 10 included (4♣, 6♣, 10♥, J♥, Q♠)
(keep the QJ)
Best Casino list that You Can Try!
Odds Of Getting A Royal Flush On The Flop
100% up to $/€200 with Free Spins on Twin Spin Megaways
Probability Of Getting A Royal Flush Equation
Frequently Asked Questions
What is the probability of being dealt a Royal Flush?
What is the probability of getting a Royal Flush in 5-card poker?
Which Video Poker game pays the most for a Royal Flush?
Playing online, Jackpot Poker by Play’n GO pays the most for a Royal Flush. It either pays 1,000 times your stake or a minimum progressive jackpot of £5,000 if playing at the highest coin level.
Is there anything I should know about chasing a Royal Flush in Video Pokers?
Always play with the highest coin level (level 5). This makes a huge difference if you would hit the Royal Flush as you would get paid more than three times as much. Playing with this coin level you usually have to bet a minimum of £1 or £1.25 per hand.
Relevant news
How to Win at Baccarat – All You Need to Know About Beating the Game
Just like Roulette and Slot Machines, Baccarat is a casino game that revolves around luck.…
read more +How to Become a Professional Poker Player
Since the poker boom hit in 2003, TV-shows such as “High Stakes Poker” have been…
read more +Why Can’t I Claim the Welcome Bonus With Skrill?
Being a casino enthusiast with a liking for e-Wallets, we’ve all been there. We go…
read more +Full Guide on How to Play Baccarat Online and the Rules of Baccarat
Baccarat is a simple and fast paced game that has been played for more than…
read more +How to Play and Win Big at Penny Slots – Full Guide Explaining Everything You Need to Know
If you’re someone who believes that it’s impossible to win at penny slots in the…
read more +The Luckiest Place to Buy a Lottery Ticket Online
It’s no secret that it’s incredibly difficult to win the lottery - at least so…
read more +Some months ago I came across the Twitch streamer Joshimuz who has quite an interesting project: He tries to play through GTA San Andreas by solving everything. Not only he tries to achieve 100 % but he also set his own goals and challenges. At the same time, he gives insights into a lot of (speed running) techniques, interesting bugs and a little bit of game development. If you like content like that, you should definitely check out his video series True 100%+ on Youtube.
Anyway, one of his goals is to get a Royal Flush in GTA's video poker. Like in normal video poker, you get 5 cards and you decide which cards you want to keep. Then, you get new cards and depending on what kind of hand you have, you get some amount of money or nothing at all. Obviously, a Royal Flush gives you the most money but is also the least likely outcome. You can watch his first attempts here.
I wondered, how much does he have to play to get a Royal Flush? How likely (in terms of probability) is it if he uses the best strategy?
tl;dr
By using the best strategy, the probability of getting a Royal Flush is about 0.0043 % which means, it's expected that he plays around 23081 games of video poker.
Furthermore, we can provide the amount of games needed for getting a Royal Flush with a certain probability. For example: It's 50 % likely that Joshimuz gets a Royal Flush if he plays 15998 games. On the other hand, there is a 1 % chance that he might not get a Royal Flush even after 106288 games.
| p | n |
|---|---|
| 1 % | 232 |
| 10 % | 2432 |
| 25 % | 6640 |
| 50 % | 15998 |
| 75 % | 31996 |
| 90 % | 53144 |
| 99 % | 106288 |
If you are interested on how to derive these results, read on!
Video Poker
Video poker uses a standard deck of 52 cards, i.e. the lowest cards are 2 , 2 , 2 , 2 and the highest cards are A , A , A , A . A Royal Flush is the highest street possible in the same suit. Therefore, there are four possible Royal Flushes, namely:
- 10BDKA
- 10BDKA
- 10BDKA
- 10BDKA
We will call these cards 'potential cards'.
For every video poker game, the player receives 5 random cards from the deck. He then can choose what he thinks are the best cards to keep and which cards should be thrown away. After that, the player receives new cards until he has 5 again and the dealer (i.e. the slot machine) evaluates the highest hand. In this problem we are not interested in getting any other winning hand like a 'Full House' or 'Three of a Kind'. Notice that you can also adjust your wagger and that there are many varieties of video poker but this not really interesting to us either.
Best Strategy
It is quite obvious that the best strategy for getting a Royal Flush is to keep potential cards (listed above) and to throw useless ones away. Sometimes, there are multiple potential cards but in different suits. Again, it's very easy to see that we should keep the suit that has more potential cards in that suit then the other. If the number is equal (for example if we have a hand like 10BKA5 ) then it does not matter if we keep or because both Royal Flushes come with the same probability.
In this post, we are not going to formally prove that this greedy strategy maximises our chances but I believe it should not be toohard.
You can take a look at the implementation of this strategy in the holdCards(hand) method at the very end.
Calculation of the Probability
Let (R) denote the event of a Royal Flush and (Omega) denote the set of all possible outcomes of drawing 5 cards from a standard deck. From the section above it's clear that there are (vert Rvert = 4) possible Royal Flushes. If we know the size of our sample space (Omega), i.e. how many ways there are to sample 5 cards from a 52 deck, we can easily calculate the probability by utilising this formula:
[Pr(text{event}) = frac{text{number of outcomes in event}}{text{number of outcomes in sample space}}]Luckily, there exists the Binomial Coefficient (binom{n}{k}) that gives us the number of possibilities of choosing (k) elements from a set of size (n) without respecting the order. Here, we have (n = 52) cards and we choose (k = 5) cards from them. By employing the formula above we get
[Pr(R) = frac{ R }{ Omega } = frac{4}{binom{52}{5}} = frac{1}{649740} approx 0.00015%]However, our problem is a bit more complicated because we completely neglected that we can optimise our chances by keeping potential cards. So far we only calculated the probability of getting a Royal Flush when we are not allowed to keep cards. From now, (R) will refer to the actual problem and not to this simple one.
Law of Total Probability, Random Variables, …
As it turns out, we need to divide our event (R) into smaller disjoint subsets. The intuition behind doing that is that it is much more likely to get a Royal Flush if the player keeps 4 potential cards in the same suit than keeping only one or two. However, drawing 4 potential cards in the same suit in the first place is much less likely than getting maybe only one. By splitting up (R) we can exactly describe this observation mathematically. This trick is known as the Law of total probability:
[Pr(A) = sum_n Pr(B_n) cdot Pr(A ;vert; B_n)]I will shortly explain what the bar inside (Pr(A ;vert; B_n)) means, but first, we also have to change our notation a bit by using Random Variables. A Random Variable is usually a function (Xcolon Omega to mathbb{R}) that maps events to natural numbers. That way, we can describe events more easily and work with them. Let (X) be a Random Variable that denotes the number of cards a player exactly kept by using the described strategy. It's clear that the kept cards are all equal or above the rank 10 and all have the same suit. In addition, (X) can only take values between 0 (not keeping any cards) and 5 (keeping all cards, aka. a Royal Flush). To refer to the probability of getting a Royal Flush if the player already holds 3 cards, we write
[Pr(R;vert;X=3)]Probabilities that come with a condition are called Conditional Probabilities where the condition is written after the bar (vert). Here we used the notation involving the Random Variable (X). If we want to refer to the probability of being able to keep three cards in the first place, we would write
[Pr(X=3)]Notice that it means something completely different. It should not be too hard to see that
[0 < Pr(R;vert;X=0) < Pr(R;vert;X=1) < dotsb < Pr(R;vert;X=5) = 1]but
[1 > Pr(X=0) > Pr(X=1) > dotsb > Pr(X=5) > 0]What Are The Odds Of Getting A Royal Flush
Since we said that (X) exactly represents the number of kept cards in a game, the associated events are disjoint and we can apply the Law of Total Probability:
[Pr(R) = sum_{x=0}^5 Pr(X=x) cdot Pr(R ;vert; X=x)]So if we find out how to calculate (Pr(X=x)) and (Pr(R ;vert; X=x)) for a given (x), we are done! We will start with the easier factor (Pr(R ;vert; X=x)).
Suppose we already hold (x) cards…
Surely there are only (52-5) cards left in deck, our hand has (x) cards and we need to draw the remaining (5-x) cards to have a full hand again. This sounds exactly like the situation at the very beginning but now, (n) is (52-5=47) and (k) is (5-x). Additionally, we need to think about the number of outcomes in the Royal Flush event (R) depending on (x). If we don't hold any card, we did not get any potential card and we could still draw any of the four possible Royal Flushes with the remaining (47) cards in the deck. But, if we save at least one card, there is only one possible Royal Flush left since we sort of 'decided' on a suit already. Therefore
[Pr(R ;vert; X=x) = begin{cases} frac{4}{binom{52-5}{5}} &text{if } x=0 frac{1}{binom{52-5}{5-x}} &text{otherwise}end{cases}]It's always a good idea to test a model for some edge cases to detect errors. We would expect that if we keep (x=5) cards, we must have a Royal Flush. Indeed this is true:
[Pr(R ;vert; X=5) = frac{1}{binom{52-5}{5-5}} = frac{1}{binom{47}{0}} = frac{1}{1} = 1]Let's tackle (Pr(X=x)).
One Random Variable is not enough
It looked easier than it was to be honest, because we have to make sure that we don't count some events twice or not at all. For example, suppose we have a hand (outcome) like this:
It's important that this outcome only counts when (x = 3) and not (x = 2). Otherwise, our subsets would not be disjoint and we could not apply the Law of Total Probability. But a lot of the simpler approaches and formulas just don't care about that and manually excluding situations like these is error prone and not convincing. This problem does not occur in the previous section because we throw cards away.
Instead, we split up (R) now a bit differently to be able to use a more systematic approach. Let (X) still be the Random Variable that keeps track of the number of cards a player wants to hold. Now, let (A) be a Random Variable that notes the number of potential cards in the current hand of a different suit than the cards being tracked by (X). In the hand above, we would have an event where (X=3) and (A=2). Let (B) and (C) be Random Variables too, where the former represents the third different suit and the latter represents the fourth different suit. Since the hand above does not have a third or fourth suit, we simply have (B=0) and (C=0). Also notice the number of non-potential cards is (5-X-A-B-C), i.e. simply the rest.
By using only (X), (A), (B) and (C) we can describe any relevant event for us, but first, we must enforce additional constraints to make all events disjoint: First, we must not exceed 5 cards on a hand and second, there must be an ordering of the Random Variables because we have to make sure that we do not get accidentally a better hand by not saving (X) cards.
- Constraint: (X+A+B+C le 5)
- Constraint: (X ge A ge B ge C ge 0)
Let's give some examples to make it clearer.
| (X) | (A) | (B) | (C) | Example Hand | Valid? |
|---|---|---|---|---|---|
| 2 | 1 | 0 | 0 | 69DKK | yes |
| 1 | 1 | 1 | 1 | 51010AA | yes |
| 5 | 0 | 0 | 0 | 10BDKA | yes |
| 4 | 2 | 0 | 0 | 10BDDKK | no, violates constraint 1 |
| 2 | 3 | 0 | 0 | 10BDKA | no, violates constraint 2 |
We need to rewrite (Pr(R)) though since we are dealing with new Random Variables now:
[Pr(R) = sum_{scriptstyle x+a+b+c le 5atopscriptstyle x ge a ge b ge c ge 0} Pr(X=x, A=a, B=b, C=c) cdot Pr(R ;vert; X=x, A=a, B=b, C=c)]So do we have to throw (Pr(R ;vert; X=x)) away, because it does not take (A), (B) and (C) into account? No we don't! Since we throw the cards tracked by (A), (B) and (C) away anyway, the probability of getting a Royal Flush does not depend on them and we do have
[Pr(R ;vert; X=x, A=a, B=b, C=c) = Pr(R ;vert; X=x)]The big question is, how do we calculate (Pr(X=x, A=a, B=b, C=c))? To do this, again, we need to think about the number of outcomes in the event and the number of outcomes in the sample space.
More combinatorics

The size of our sample space (Omega) is (binom{52}{5}) again since we start with a fresh deck and then draw 5 cards from it.
To determine the number of outcomes in the event (X=x, A=a, B=b, C=c), we need to consider all different combinations of suits together with all different combinations of ranks. To make it easier first, let's fix the Random Variables to one specific suit: (X) tracks , (A) tracks , (B) tracks and (C) tracks . Let (r(x, a, b, c)) represent the number of different rank combinations. If suits are fixed,
[Pr(X=x, A=a, B=b, C=c) = frac{r(x, a, b, c)}{binom{52}{5}}]Finding a term for (r(x, a, b, c)) is easy. Think about you have 5 different decks:
- 5 potential cards of suit
- 5 potential cards of suit
- 5 potential cards of suit
- 5 potential cards of suit
- 32 other (useless) cards of any suit
Now we draw (x) cards from the deck, (a) cards from the deck, (b) cards from the deck, (c) cards from the deck and the missing (5-x-a-b-c) cards from the other cards:
[r(x, a, b, c) = binom{5}{x} cdot binom{5}{a} cdot binom{5}{b} cdot binom{5}{c} cdot binom{32}{5-x-a-b-c}]Sadly (luckily?), our Random Variables can track any suit and it only matters, that two Random Variables do not track the same suit at the same time. Therefore, we have to calculate (r(x, a, b, c)) for any possible suit as well. Let (s(x, a, b, c)) denote the number of suit combinations. We then can simply multiply those two terms.
[Pr(X=x, A=a, B=b, C=c) = frac{ s(x, a, b, c) cdot r(x, a, b, c)}{binom{52}{5}}]Finding a nice term for (s(x, a, b, c)) is a bit more tricky, but there are some observations: At first, we have four different possibilities to assign a suit to (X). Because (A) has to be a different suit than (X), there are only three possibilities left. The same applies for (B) and once we assigned suits to (X), (A) and (B) already, there is only one possibility left for (C). If our event consists of only two suits, we simply neglect the possibilities for the other two suits. In the equation below, (H(x)) is a 'left-continuous' Heaviside step function that is (0) if (x) is (0) and is (1) if (x>0).
[s(x, a, b, c) = frac{4^{H(x)} cdot 3^{H(a)} cdot 2^{H(b)} cdot 1^{H(c)}}{g(x, a, b, c)}]So what is (g(x, a, b, c)) doing? The enumerator sometimes counts suit combinations twice or more times but sometimes does not. On the one hand, the event (X=2, A=1, B=0, C=0) has following combinations:
[], [], [], [], [], [], [], [], [], [], [], []
On the other hand, the event (X=1, A=1, B=0, C=0) has much fewer:
[], [], [], [], [], []
If two/three/four Random Variables share the same number as others and are at least (1) (here: (A = X = 1)), we need to remove additional counted outcomes due to permutations. We do this by using factorials. (n!) is the number of ways how to permute (n) elements. For instance (n=3), we would get (n! = 3 cdot 2 cdot 1 = 6) different ways to permute three suits:
[], [], [], [], [], []
The easiest way to find out (g(x, a, b, c)) is to simply go through every valid assignment for (X=x, A=a, B=b, C=c) and think about it directly. In many cases it is just 1.
| Example | (C) | (B) | (A) | (X) | (g) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 2 | |
| 0 | 1 | 1 | 1 | 6 | |
| 1 | 1 | 1 | 1 | 24 | |
| 0 | 0 | 0 | 2 | 1 | |
| 0 | 0 | 1 | 2 | 1 | |
| 0 | 1 | 1 | 2 | 2 | |
| 1 | 1 | 1 | 2 | 6 | |
| 0 | 0 | 2 | 2 | 2 | |
| 0 | 1 | 2 | 2 | 2 | |
| 0 | 0 | 0 | 3 | 1 | |
| 0 | 0 | 1 | 3 | 1 | |
| 0 | 1 | 1 | 3 | 2 | |
| 0 | 0 | 2 | 3 | 1 | |
| 0 | 0 | 0 | 4 | 1 | |
| 0 | 0 | 1 | 4 | 1 | |
| 0 | 0 | 0 | 5 | 1 |
We are finally in a position where we can calculate (Pr(X=x, A=a, B=b, C=c))! Let's do it:
| Example | (C) | (B) | (A) | (X) | (Pr(X=x, A=a, B=b, C=c)) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 7.75 % | |
| 0 | 0 | 0 | 1 | 27.67 % | |
| 0 | 0 | 1 | 1 | 28.63 % | |
| 0 | 1 | 1 | 1 | 9.54 % | |
| 1 | 1 | 1 | 1 | 0.77 % | |
| 0 | 0 | 0 | 2 | 7.63 % | |
| 0 | 0 | 1 | 2 | 11.45 % | |
| 0 | 1 | 1 | 2 | 3.69 % | |
| 1 | 1 | 1 | 2 | 0.19 % | |
| 0 | 0 | 2 | 2 | 0.74 % | |
| 0 | 1 | 2 | 2 | 0.23 % | |
| 0 | 0 | 0 | 3 | 0.76 % | |
| 0 | 0 | 1 | 3 | 0.74 % | |
| 0 | 1 | 1 | 3 | 0.12 % | |
| 0 | 0 | 2 | 3 | 0.05 % | |
| 0 | 0 | 0 | 4 | 0.02 % | |
| 0 | 0 | 1 | 4 | 0.01 % | |
| 0 | 0 | 0 | 5 | 0.0002 % | |
| Sum | 100 % |
We quickly confirm our calculation by summing up all (p(X=x, A=a, B=b, C=c)). If we would not get (1) back, that would mean some events count outcomes too much or not at all.
[sum_{scriptstyle x+a+b+c le 5atopscriptstyle x ge a ge b ge c ge 0} p(X=x, A=a, B=b, C=c) = 1]We are almost done.
Putting everything together
Since I also wanted to know (Pr(X=x)), I simply added all disjoint subset satisfying (X=x) together, like this:
[Pr(X=4) = Pr(X=4, A=0, B=0, C=0) + Pr(X=4, A=1, B=0, C=0)]These are my results
| Example | (X) | (Pr(X=x)) | (Pr(R ;vert; X=x)) |
|---|---|---|---|
| 0 | 7.75 % | 0.0003 % | |
| 1 | 66.61 % | 0.001 % | |
| 2 | 23.94 % | 0.01 % | |
| 3 | 1.66 % | 0.09 % | |
| 4 | 0.04 % | 2.13 % | |
| 5 | 0.0002 % | 100 % | |
| Sum | 100 % |
Finally, by using Law of Total Probability:
[Pr(R) = sum_{x=0}^5 Pr(X=x) cdot Pr(R ;vert; X=x) approx frac{1}{23081} approx 0.0043 %]Number of expected games and more
Let (E) denote the expected number of games we need to play until we get a Royal Flush. If we get one, we stop. Otherwise we try again. Read this for details.
[E = 1 + frac{23080}{23081} cdot E Rightarrow E = 23081]This does not tell us that much because it rather means, on average we need 23081 games. However, I am pretty sure we don't want to get Royal Flushes a second or third time. There is something else we can do: We could provide a probability (p) on how likely it is that we get a Royal Flush in the first (n) tries.
With the help of complementary events we solve for (n):
[p = 1 - (1-Pr(R))^n Leftrightarrow 1-p = (1-Pr(R))^n Leftrightarrow ln{(1-p)} = n ln{(1-Pr(R))}][Leftrightarrow n = frac{ln(1-p)}{ln(1-Pr(R))}]I think this table describes much better how much effort Josh might have to put into his project.
| p | n |
|---|---|
| 1% | 232 |
| 10% | 2432 |
| 25% | 6640 |
| 50% | 15998 |
| 75% | 31996 |
| 90% | 53144 |
| 99% | 106288 |
Empirical Validation
To confirm the theory, I wrote a small Python script that simulates getting a Royal Flush 10000 times. After 4h on my MacBook, the probability was (0.0042%), which is not too far away from (0.0043 %). You can find the code below:
Update: In case you come up with a better way, please let me know.
Update: @MrSmithVP simulated this already here using C++ and a more efficient implementation.
Update: Joshimuz mentioned my blog post in one of his videos. Thanks!
Update: 'He did it!' See comments or this Reddit thread.